Spatial discretization of the governing equations
We discretize both the Stokes and heat diffusion equations using a Finite Differences approach on a staggered grid (ref Taras book here).
Heat diffusion
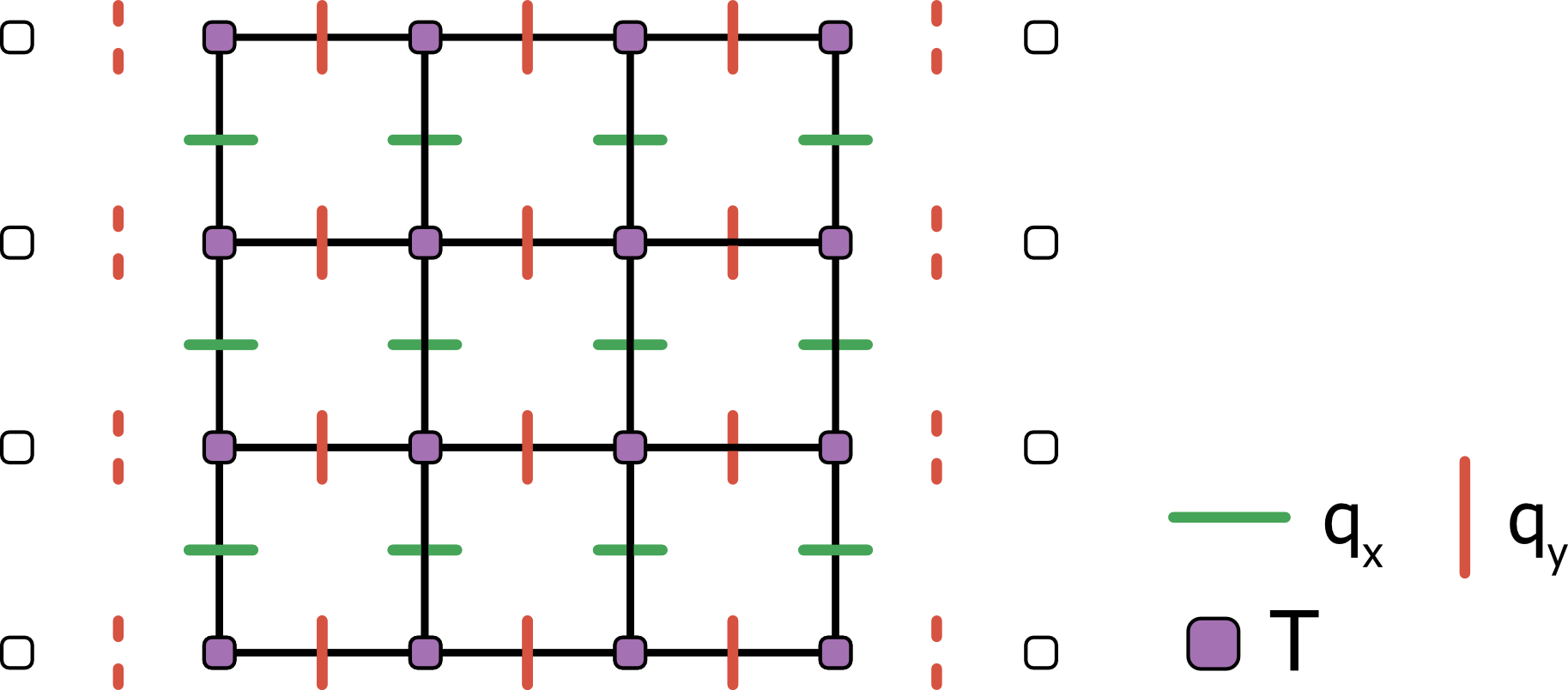
Stokes equations
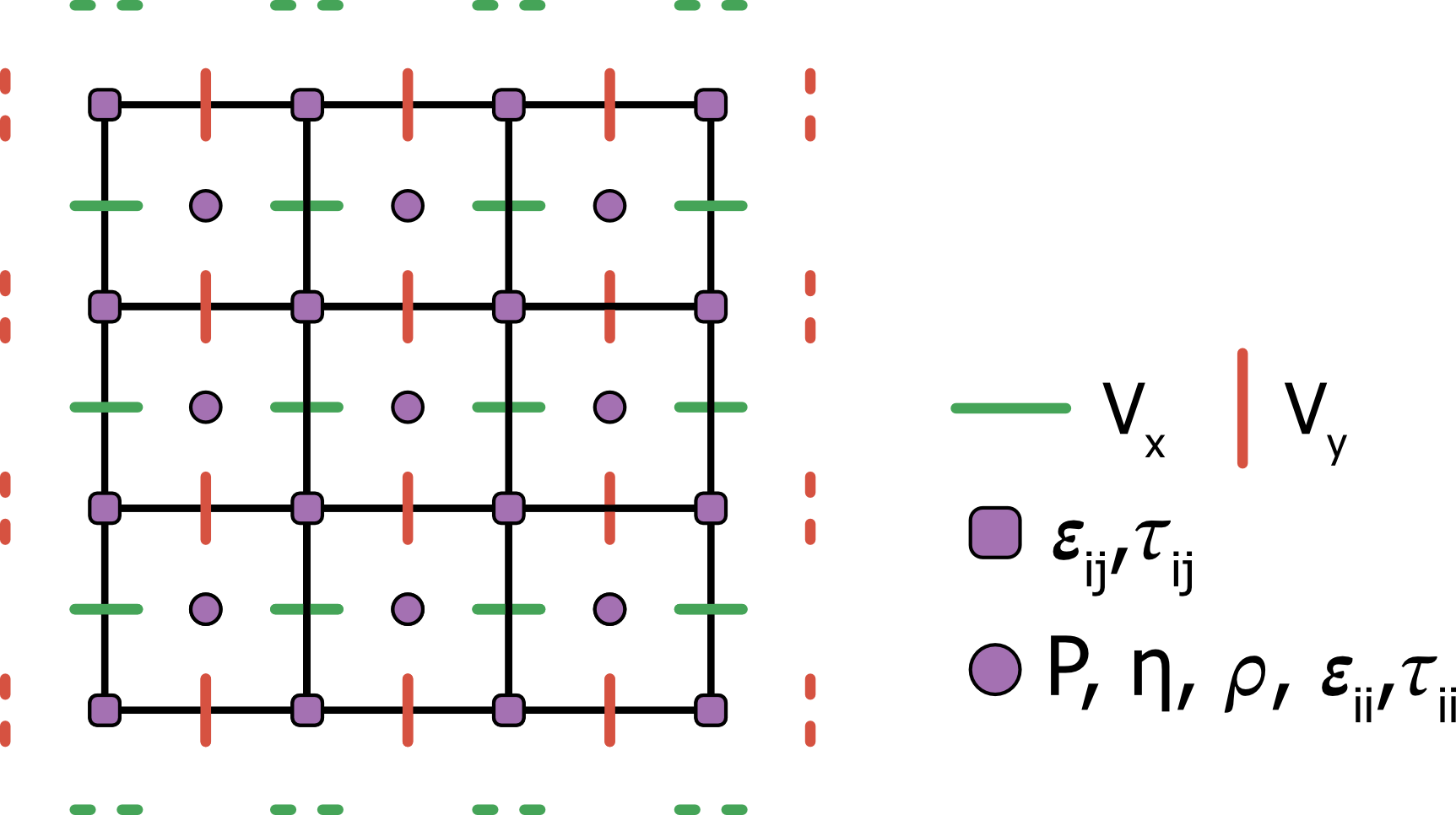 where dotted lines represent the velocity ghost nodes.
where dotted lines represent the velocity ghost nodes.
Time and pseudo-time discretization of the APT equations
We discretize both the Stokes and heat diffusion equations using a Finite Differences approach on a staggered grid (ref Taras book here).
Heat diffusion
Upon convergence we recover