Grids

The choice of numerical grid used depends on the type of equations to be resolved and affects the discretization schemes used. The design of the Chmy.Grids module aims to provide a robust yet flexible user API in customizing the numerical grids used for spatial discretization.

We currently support grids with quadrilateral cells. An N-dimensional numerical grid contains N spatial dimensions, each represented by an axis.

Grid Properties	Description	Tunable Parameters
Dimensions	The grid can be N-dimensional by having N axes.	`AbstractAxis`
Distribution of Nodal Points	The grid can be regular (uniform distribution) or non-regular (irregular distribution).	`UniformAxis`, `FunctionAxis`
Distribution of Variables	The grid can be non-staggered (collocated) or staggered, affecting how variables are positioned within the grid.	`Center`, `Vertex`

Axis

Objects of type AbstractAxis are building blocks of numerical grids. We can either define equidistant axes with UniformAxis, or parameterized axes with FunctionAxis.

Uniform Axis

To define a uniform axis, we need to provide:

Origin: The starting point of the axis.
Extent: The length of the section of the axis considered.
Cell Length: The length of each cell along the axis.

With the information above, an axis can be defined and incorporated into a spatial dimension. The spacing (with alias Δ) and inv_spacing (with alias iΔ) functions allow convenient access to the grid spacing (Δx/Δy/Δz) and its reciprocal, respectively.

Function Axis

As an alternative, one could also define a FunctionAxis object using a function that parameterizes the spacing of the axis, together with the length of the axis.

f = i -> ((i - 1) / 4)^1.5
length = 4
parameterized_axis = FunctionAxis(f, length)

Structured Grids

A common mesh structure that is used for the spatial discretization in the finite difference approach is a structured grid (concrete type StructuredGrid or its alias SG).

We provide a function UniformGrid for creating an equidistant StructuredGrid, that essentially boils down to having axes of type UniformAxis in each spatial dimension.

# with architecture as well as numerics lx/y/z and nx/y/z defined
grid   = UniformGrid(arch;
                    origin=(-lx/2, -ly/2, -lz/2),
                    extent=(lx, ly, lz),
                    dims=(nx, ny, nz))

Metal backend

If using the Metal backend, ensure to use Float32 (f0) element types in the origin and extent tuples when initialising the grid.

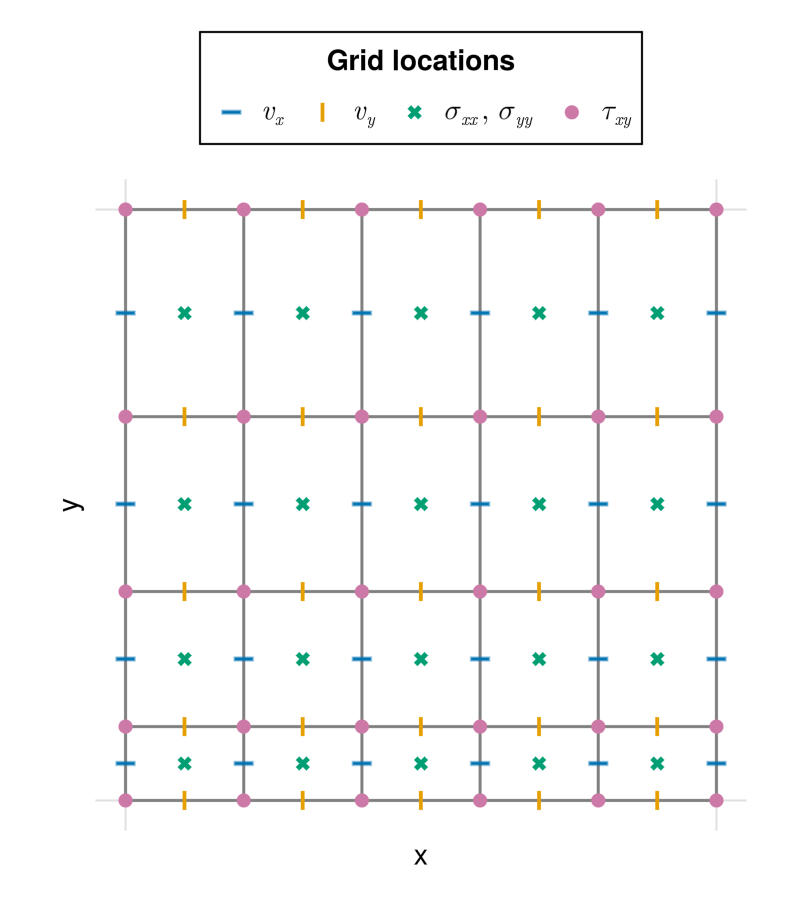
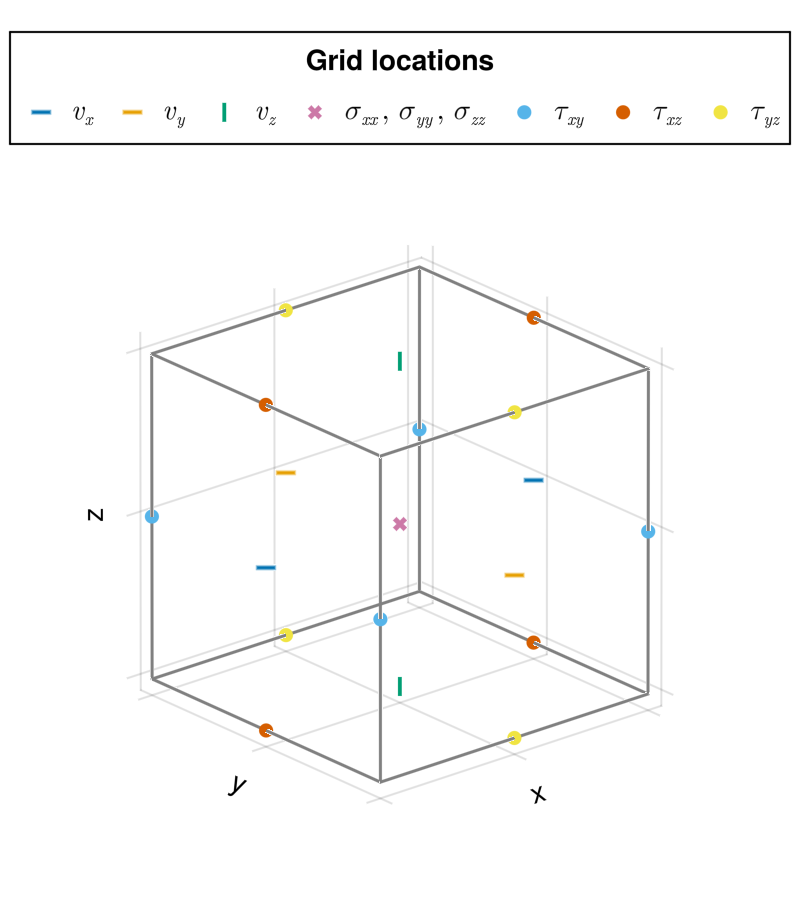
Interactive Grid Visualization

grids_2d.jl: Visualization of a 2D StructuredGrid
grids_3d.jl: Visualization of a 3D StructuredGrid

Location on a Grid Cell

In order to allow full control over the distribution of different variables on the grid, we provide a high-level abstraction of the property location on a grid cell with the abstract type Location. More concretely, a property location along a spatial dimension can be either of concrete type Center or Vertex on a structured grid.

We illustrate how to specify the location within a grid cell on a fully staggered uniform grid. The following 2D example also has ghost nodes illustrated that are located immediately outside the domain boundary.

In the following example, we zoom into a specific cell on a fully-staggered grid. By specifying for both x- and y-dimensions whether the node locates at the Center (C) or Vertex (V) along the respective axis, we can arrive in 4 categories of nodes on a 2D quadrilateral cell, which we refer to as "basic", "pressure", "Vx" and "Vy" nodes, following common practices.

If all variables are defined on basic nodes, specified by (V,V) locations, we have the simplest non-staggered collocated grid.

Dimensions of Fields on Structured Grids

With a structured grid defined that consists of nx = N cells horizontally and ny = M cells vertically, we have the following dimensions for fields associated with the grid.

Node Type	Field Dimension	Location
Cell vertex	$(N + 1) \times (M + 1)$	`(V, V)`
X interface	$(N + 1) \times M$	`(V, C)`
Y interface	$ N \times (M + 1)$	`(C, V)`
Cell Center	$N \times M$	`(C, C)`

Connectivity of a `StructuredGrid`

Using the method connectivity(::SG{N,T,C}, ::Dim{D}, ::Side{S}), one can obtain the connectivity underlying a structured grid. If no special grid topology is provided, a default Bounded grid topology is used for the UniformGrid. Therefore, on a default UniformGrid, the following assertions hold:

julia> @assert connectivity(grid, Dim(1), Side(1)) isa Bounded "Left boundary is bounded"

julia> @assert connectivity(grid, Dim(1), Side(2)) isa Bounded "Right boundary is bounded"

julia> @assert connectivity(grid, Dim(2), Side(1)) isa Bounded "Upper boundary is bounded"

julia> @assert connectivity(grid, Dim(2), Side(2)) isa Bounded "Lower boundary is bounded"